Sensor measurement function
Uncertainty analysis and metrological traceability should start with the measurement function. Here, the word ‘measurement’ must be considered in its broadest sense and includes the concept of an indirect measurement, where an indicated quantity (e.g. a signal count) is transformed to the measurand (e.g. radiance), which is the quantity intended to be measured.
The measurement function is defined from the ‘measurement model’, which establishes the mathematical relations between the measurand () and the input quantities (). Here, we use the word ‘function’ in the most general sense. Often, we can explicitly write the measurement model in terms of an analytic expression of quantities:
![]()
where:
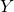 epresents the output quantity (the measurand)
epresents the output quantity (the measurand)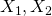 are the input quantities, for example, the counts
are the input quantities, for example, the counts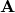 is the vector of calibration parameters (which are also input quantities but are usefully distinguished)
is the vector of calibration parameters (which are also input quantities but are usefully distinguished)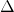 is an input quantity introduced to represent any inadequacy of the function f to represent all phenomena that affect the measurand
is an input quantity introduced to represent any inadequacy of the function f to represent all phenomena that affect the measurand
Sometimes it is necessary to define the measurement function in a different way, for example as the iterative solution of a measurement model through code.
The equations used to populate e.g. L1 products, evaluate the measurand using estimates of the input quantities. In the GUM, the convention is for estimates to be represented with the lower-case characters corresponding to the quantities written in upper case. The measured output value is therefore determined from the expression:
![]()
where the input estimates include the recorded sensor counts and values of calibration coefficients, etc. Since 0 is our best estimate of ![]() , which is the expectation of
, which is the expectation of ![]() (assuming we are using the best measurement model we can formulate), then we may practically write this as
(assuming we are using the best measurement model we can formulate), then we may practically write this as
![]()
Here, this ‘plus zero’ term does not alter the value of the measurand, but will have an associated uncertainty in recognition of the fact that all measurement functions are approximations to the physical process they describe. In other words, this term considers the extent to which the equality of the measurement function may not hold. For example:
- If the measurement function is a linear equation, the ‘plus zero’ term considers the extent to which the instrument may be non-linear.
- If the measurement function is a spectral integral determined numerically using a trapezium or rectangular rule, the ‘plus zero’ term considers the extent to which this rule acts as an approximation of the integrated quantity.
- If there is an assumption that quantities or effects cancel each other out, the ‘plus zero’ term considers the uncertainty in the extent to which they cancel
- If there is an assumption that the effects of stray light are negligible, the ‘plus’ zero’ term considers the extent to which the assumption is valid
Once we have a clear picture of the extent to which the measurement function describes the true physical state of the measurement process and the effects that influence each input quantity, we can determine the uncertainty in the measurand through the process of uncertainty analysis.
Error effects
Each input quantity in the measurement function (whether written formally as in ![]() , or as it is calculated, as in
, or as it is calculated, as in ![]() ), has associated with it at least one source of error. This includes measured counts, calibration parameters (for Level 1) or retrieval parameters (for level 2) and the “plus zero” or term.
), has associated with it at least one source of error. This includes measured counts, calibration parameters (for Level 1) or retrieval parameters (for level 2) and the “plus zero” or term.
It is important to identify and consider each of these error effects in turn. Every error effect is a source of uncertainty and we should quantify the size of that uncertainty, and understand the sensitivity coefficient (the ‘translation’ between an error in the input quantity and the error in the output quantity). For example, if an error effect affects the input quantity ![]() and has an uncertainty
and has an uncertainty ![]() , then the uncertainty associated with due to this effect is given by
, then the uncertainty associated with due to this effect is given by ![]() , where
, where ![]() is the sensitivity coefficient.
is the sensitivity coefficient.
We should also consider the error correlation introduced by the effect by considering the influence of a single error in that input quantity on spatial and temporal scales.
Error correlation
Independent, structured and common errors, correlation
The measured value in each pixel of an EO image is the result of a sequence of steps and transformations. In transforming from raw data (L0) to calibrated radiances (L1), many measured values relevant to calibration measurements may be combined. In transforming L1 radiances to L2 geophysical products radiances from different spectral bands may be used. In L2 to L3+ processing, data across different pixels are then combined. (This description is biased towards radiometric sensors; similar principles apply in altimetry). Where correlation exists between errors in different measured values (different wavelengths and/or pixels), this error correlation needs to be considered in the uncertainty analysis.
The GUM defines systematic and random errors, concepts that are widely used in science.
Random errors are errors manifesting independence: the error in one instance is in no way predictable from knowledge of the error in another instance. A complication arises in EO imagery when one instance of a parameter in the radiance measurement function is used in the calculation of the Earth radiance across many pixels. That component of the error in the radiance image is then correlated across pixels, even though the originating effect is random. Put another way, the originating random error contributes errors with a particular structure to the image.
Systematic errors are those that could in principle be corrected for if we had sufficient information to do so: that is, they arise from unknowns that could in principle be estimated rather than from chance processes. All systematic errors in EO are structured in that there is a pattern of influence on multiple data. They include, but are not limited to, effects that are constant for a significant proportion of a satellite mission—i.e., biases, for which the structure is a simple error in common.
When considering EO imagery, it is can be useful to categorise effects primarily according to their cross-pixel error correlation properties, as independent, structured or common effects.
Independent errors
Independent errors arise from random effects causing errors that manifest independence between pixels, such that the error in ![]() is in no way predictable from knowledge of the error in
is in no way predictable from knowledge of the error in ![]() , were that knowledge available. Independent errors therefore arise from random effects operating on a pixel level, the classic example being detector noise.
, were that knowledge available. Independent errors therefore arise from random effects operating on a pixel level, the classic example being detector noise.
Structured errors
Structured errors arise from effects that influence more than one measured value in the satellite image, but are not in common across the whole image. The originating effect may be random or systematic (and acting on a subset of pixels), but in either case the resulting errors are not independent, and may even be perfectly correlated across the affected pixels. Since the sensitivity of different pixels/channels to the originating effect may differ, even if there is perfect error correlation, the error (and associated uncertainty) in the measured radiance can differ in magnitude. Structured errors are therefore complex, and, at the same time, important to understand, because their error correlation properties affect how uncertainty propagates to higher-level data.
Common errors
Common errors are constant (or nearly so) across the satellite image, and may be shared across the measured radiances for a significant proportion of a satellite mission. Common errors might typically be referred to as biases in the measured radiances. Effects such as the progressive degradation of a sensor operating in space mean that such biases may slowly change.
Further material:
- FIDUCEO tutorials
- Mittaz, C. Merchant, E. Woolliams “Applying Principles of Metrology to Historical Earth Observations from Satellites”, 2019. (under review at Metrologia, paper expected to be published soon)

Recent Comments